有限元分析 (FEA) 是使用稱為有限元法 (FEM) 的數值技術模擬任何給定的物理現象。
工程師使用FEA減少物理原型和實驗的數量,并在設計階段優化組件,以更快地開發更好的產品,同時節省開支。
有必要使用數學來全面理解和量化任何物理現象,例如結構或流體行為、熱傳輸、波傳播、等。大多數這些過程都使用偏微分方程 (PDE) 來描述。然而,對于求解這些偏微分方程的計算機,數值技術在過去幾十年得到了發展,而當今最突出的技術之一就是有限元分析。
微分方程不僅描述自然現象,也描述工程力學中遇到的物理現象。
這些偏微分方程 (PDE) 是復雜的方程,需要求解這些方程才能計算結構的相關量 以估計給定載荷下的結構行為。重要的是要知道 FEA 僅給出問題的近似解,并且是獲得這些偏微分方程的真實結果的數值方法。
簡而言之,FEA 是一種數值方法,用于預測零件或裝配體在給定條件下的行為方式。
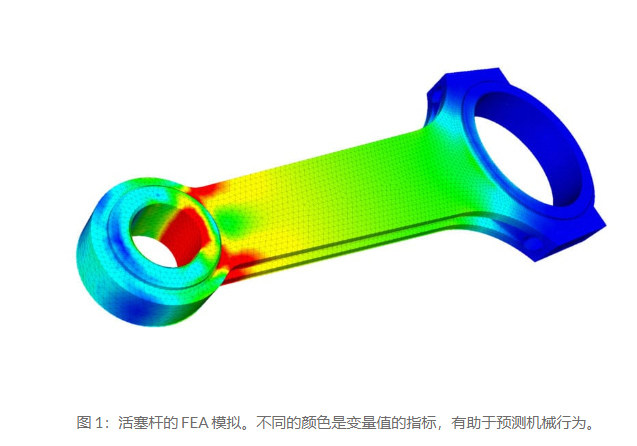
它被用作現代仿真軟件的基礎,幫助工程師找到設計中的弱點、緊張區域等。基于 FEA 方法的模擬結果通常通過色標來描述,例如顯示物體上的壓力分布。
分步解決
為了能夠進行模擬,需要創建一個由多達數百萬個共同構成結構形狀的小元素組成的網格。對每個元素進行計算。結合各個結果給我們結構的最終結果。我們剛才提到的近似值通常是多項式的,實際上是對元素的插值。這意味著我們知道元素內某些點的值,但不是每個點的值。這些“特定點”稱為節點,通常位于元素的邊界處。變量變化的準確性由一些近似值表示,例如。線性、二次、三次等。為了更好地理解近似技術,我們將查看一維條形。
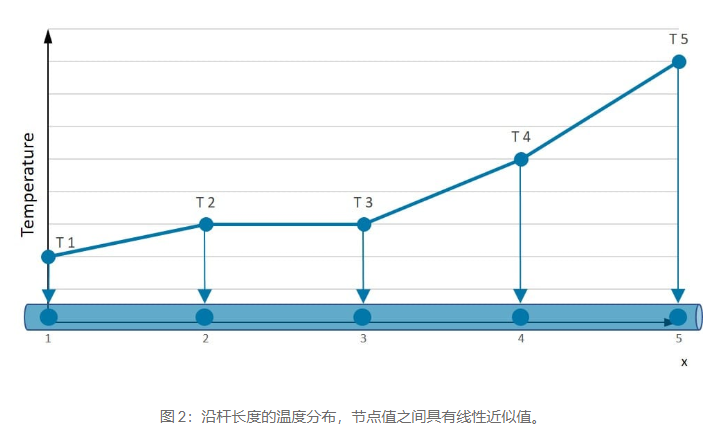
假設我們知道該條在 5 個特定位置(圖中的數字 1-5)的溫度。現在的問題是:我們如何預測這些點之間的溫度?線性近似非常好,但有更好的可能性來表示真實的溫度分布。如果我們選擇平方近似,則沿條的溫度分布會平滑得多。然而,我們看到,無論多項式次數如何,一旦我們知道節點處的值,桿上的分布就是已知的。如果我們有一個無限長的條,我們就會有無限多的未知數(自由度 (DOF))。但在這種情況下,我們遇到了“有限”數量的未知數的問題:
具有有限個未知數的系統稱為離散系統。具有無限個未知數的系統稱為連續系統。
我們在使用有限元分析時擁有的最大優勢之一是我們可以改變每個元素的離散化或離散化相應的基函數。事實上,我們可以在高梯度的區域使用較小的元素你預計。為了對函數的陡度建模,我們需要進行近似。
偏微分方程
在繼續進行 FEA 本身之前,了解不同類型的 PDE 及其對 FEA 的適用性非常重要。理解這一點對每個人都很重要,無論一個人使用有限元分析的動機如何。人們應該經常提醒自己,FEA是一種工具,任何工具的好壞取決于它的用戶。
PDE 可分為橢圓(非常平滑)、雙曲線(支持具有不連續性的解)和拋物線(描述時間相關的擴散問題)。在求解這些微分方程時,需要提供邊界和/或初始條件。根據 PDE 的類型,可以評估必要的輸入。每個類別中 PDE 的示例包括泊松方程(橢圓)、波動方程(雙曲線)和傅里葉定律(拋物線)。
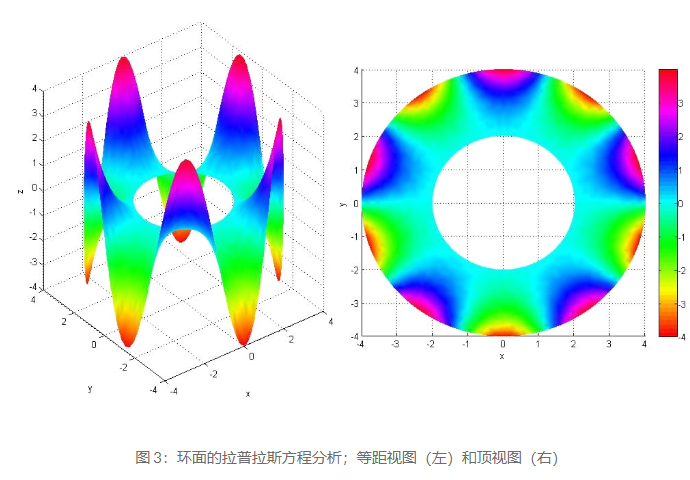
解決橢圓偏微分方程的主要方法有兩種——有限差分分析 (FDA) 和變分(或能量)方法。FEA 屬于變分法的第二類。變分方法主要基于能量最小化的哲學。
雙曲 PDE 通常與解決方案中的跳躍相關聯。例如,波動方程是雙曲 PDE。由于解中存在不連續性(或跳躍),最初的 FEA 技術(或 Bubnov-Galerkin 方法)被認為不適合求解雙曲 PDE。然而,多年來,已經進行了修改以擴展FEA軟件和技術的適用性。
重要的是要考慮使用不適合所選 PDE 類型的數值框架的后果。這種用法會導致被稱為“不正確設定”的解決方案。這可能意味著域參數的微小變化會導致解中的大振蕩,或者解僅存在于域或時間的特定部分。這些都不靠譜。適定的解決方案是用唯一的解決方案定義的,該解決方案對于定義的數據連續存在。因此,考慮到可靠性,獲得它們極為重要。
弱和強公式
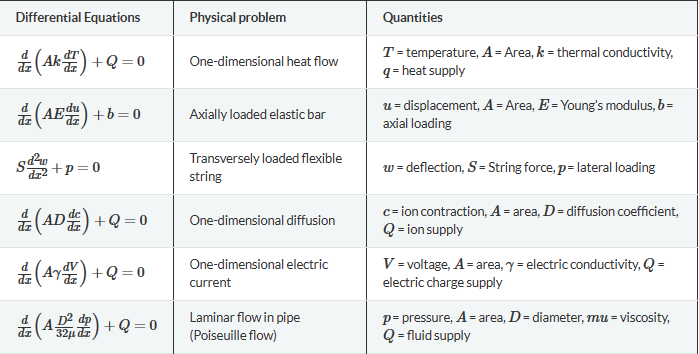
表 1:二階微分方程
二階偏微分方程的解要求高度平滑( x ). 這意味著位移的二階導數必須存在并且必須是連續的!這也意味著對幾何形狀(尖銳邊緣)和材料參數(材料中的不同模量)等參數不能受到影響的要求。
要開發有限元公式,必須以稱為弱形式的積分形式重述偏微分方程。弱形態和強形態是等價的!在應力分析中,弱式稱為虛功原理。
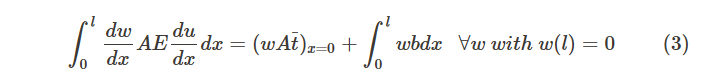
給定的方程是所謂的弱形式(在這種情況下是彈性靜力學的弱公式)。顧名思義,弱形式的解不需要像強形式的解那樣平滑,這意味著連續性要求較弱。
必須記住,滿足弱形式的解也是方程的強對應形式的解。另外,請記住試用解決方案( x )必須滿足位移邊界條件。這是試驗解的一個基本屬性,這就是為什么我們稱這些邊界條件為基本邊界條件。
最小勢能
有限元分析也可以用變分原理來執行。在一維彈性靜力學的情況下,最小勢能對于保守系統是有彈性的。平衡位置是穩定的,如果系統的勢能π是最小的。穩定位置的每一個無窮小干擾都會導致能量不利狀態,并意味著恢復反應。一個簡單的例子是立在地上的普通玻璃瓶,它的勢能最小。如果它倒下,除了一聲巨響,什么也不會發生。如果它站在桌子的??角落并掉到地上,它很可能會摔壞,因為它會將更多的能量帶向地面。對于變分原理,我們利用了這個事實。能量水平越低,得到錯誤解的可能性就越小。總勢能π系統的功由內力(應變能)組成
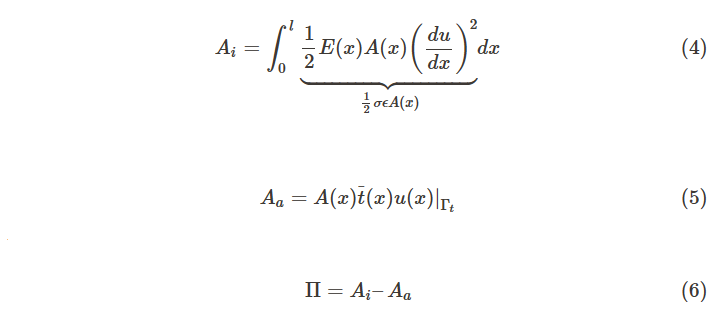
網狀融合
計算力學中影響精度的最容易被忽視的問題之一是網格收斂。這與單元需要多小有關,以確保分析結果不受更改網格大小的影響。
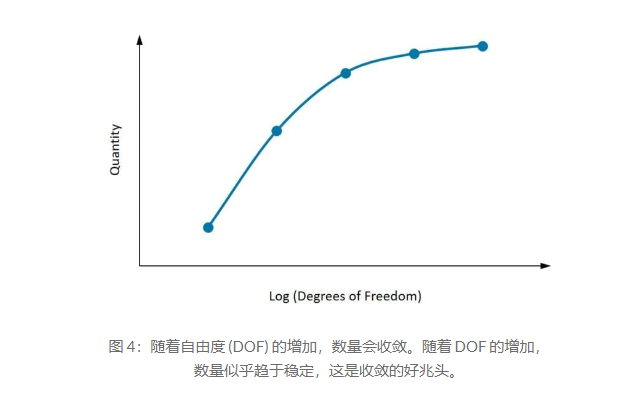
上圖顯示了一個數量隨著自由度的增加而收斂。如圖所示,首先確定感興趣的數量很重要。至少需要考慮三個點,并且隨著網格密度的增加,感興趣的數量開始收斂到特定值。如果兩個后續的網格細化沒有顯著改變結果,那么可以假設結果已經收斂。
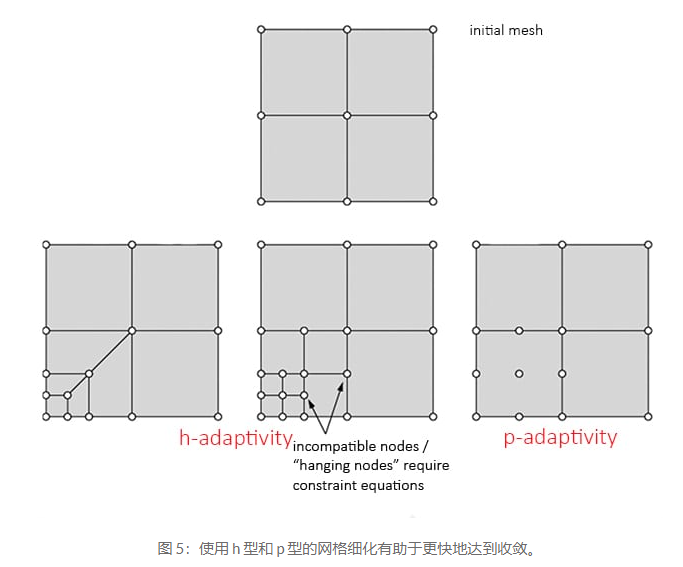
進入網格細化問題,并不總是需要細化整個模??型中的網格。圣維南原理強調一個區域的局部應力不會影響其他地方的應力。因此,從物理的角度來看,模型只能在特定的感興趣區域進行細化,并且還具有從粗網格到細網格的過渡區域。如上圖所示,有兩種類型的細化(h-和p-細化)。h-refinement 涉及減少元素大小,而 p-refinement 涉及增加元素的階數。
這里區分幾何效應和網格收斂很重要,特別是當使用直線(或線性)元素對曲面進行網格化時,需要更多元素(或網格細化)才能準確捕獲邊界。網格細化導致錯誤顯著減少:

像這樣的細化可以增加解決方案的收斂性,而不會增加要解決的整體問題的規模。
如何衡量收斂性
那么既然已經討論了收斂的重要性,那么如何衡量收斂呢?什么是收斂的量化指標?第一種方法是與解析解或實驗結果進行比較。
位移誤差:
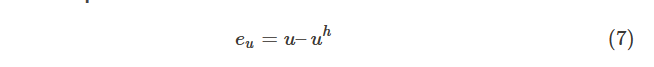
u是位移場的解析解
應變誤差:
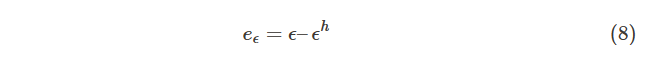
ε 是應變場的解析解
應力誤差:
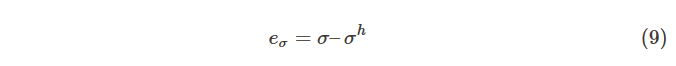
σ 是應力場的解析解
如上面的方程式所示,可以為位移、應變和應力定義多個誤差。這些誤差可用于比較,它們需要通過網格細化來減少。
有限元分析軟件

有限元分析開始于對與航空航天和土木工程相關的幾種機械應用進行建模方面的重大承諾。有限元方法的應用才剛剛開始發揮其潛力。最令人興奮的前景之一是它在流體-結構相互作用等耦合問題中的應用;熱機械、熱化學、熱化學機械問題壓電、鐵電、電磁學和其他相關領域:
靜態分析
通過靜態分析,您可以分析線性靜態和非線性準靜態結構。在施加靜載荷的線性情況下,只需一步即可確定結構響應。可以考慮幾何、接觸和材料非線性。
動態分析
動態分析可幫助您分析在特定時間范圍內經歷動態載荷的結構的動態響應。要以真實的方式對結構問題進行建模,您還可以分析載荷和位移的影響。
模態分析
振動引起的結構的特征頻率和特征模態可以使用模態分析進行模擬。結構或系統在給定負載下的峰值響應可以通過諧波分析來模擬。
想了解更多一些有限元仿真軟件可查看: CAE概念廠商及軟件介紹
不同類型的有限元方法
正如前面關于 PDE 的部分所討論的,傳統的 FEM 技術在與流體力學、波傳播等相關的建模問題中表現出不足。在過去的二十年中,已經進行了多項改進以改進求解過程并擴展有限元的適用性分析廣泛的問題類型。一些仍在使用的重要的包括:
擴展有限元法 (XFEM)
Bubnov-Galerkin 方法需要元素間位移的連續性。然而,接觸、斷裂和損壞等問題涉及有限元方法無法直接處理的不連續性和跳躍。為了克服這個缺點,XFEM 在 1990 年代誕生了。XFEM 通過使用 Heaviside 階梯函數擴展形函數來工作。額外的自由度被分配給不連續點周圍的節點,以便可以考慮跳躍。
廣義有限元法 (GFEM)
GFEM 在 90 年代與 XFEM 大約同時推出。它結合了傳統FEM軟件和無網格方法的特點。形狀函數主要在全局坐標中定義,并進一步乘以統一分區以創建局部基本形狀函數。GFEM 的優勢之一是防止圍繞奇點重新劃分網格。
混合有限元法
在一些問題中,例如接觸或不可壓縮性,約束是使用拉格朗日乘數施加的。這些由拉格朗日乘數引起的額外自由度是獨立求解的。方程式像耦合系統一樣求解。
hp-有限元法
hp-FEM 是使用自動網格細化 (h-refinement) 和增加多項式階數 (p-refinement) 的組合。這與分別進行 h- 和 p- 優化不同。當使用自動 hp-refinement 時,一個元素被分成更小的元素(h-refinement),每個元素也可以有不同的多項式階數。
間斷伽遼金有限元法 (DG-FEM)
DG-FEM 已經顯示出使用有限元的思想來解決傳統有限元方法薄弱的雙曲方程的重要前景。此外,它還在大多數材料工藝中常見的彎曲和不可壓縮問題方面顯示出希望。這里向弱形式添加了額外的約束,包括懲罰參數(以防止相互滲透)和元素之間的其他應力平衡項。
速石科技有限元分析
速石的FEA軟件組件使您能夠虛擬測試和預測結構的行為,從而解決受靜態和動態載荷條件影響的復雜結構工程問題。FEA仿真平臺使用可擴展的數值方法,可以計算數學表達式,否則由于復雜的載荷、幾何形狀或材料特性,這些表達式將非常具有挑戰性。
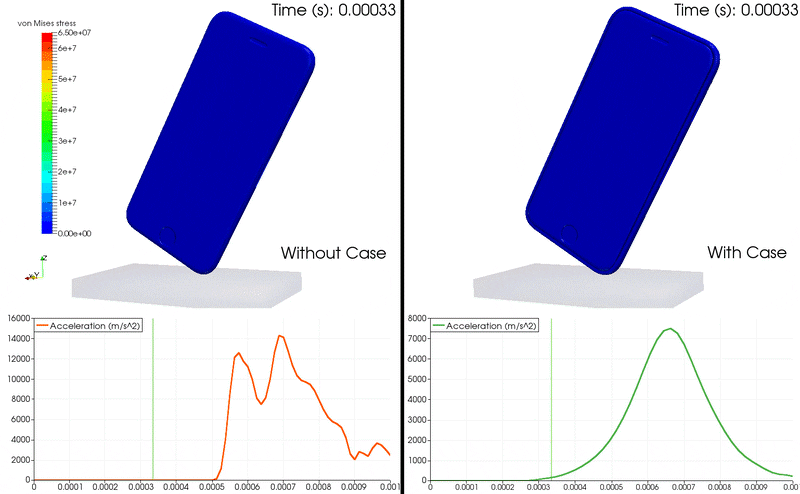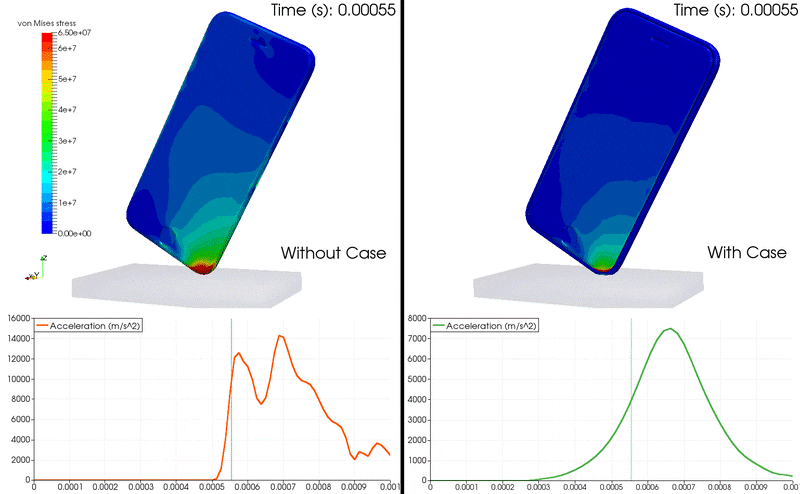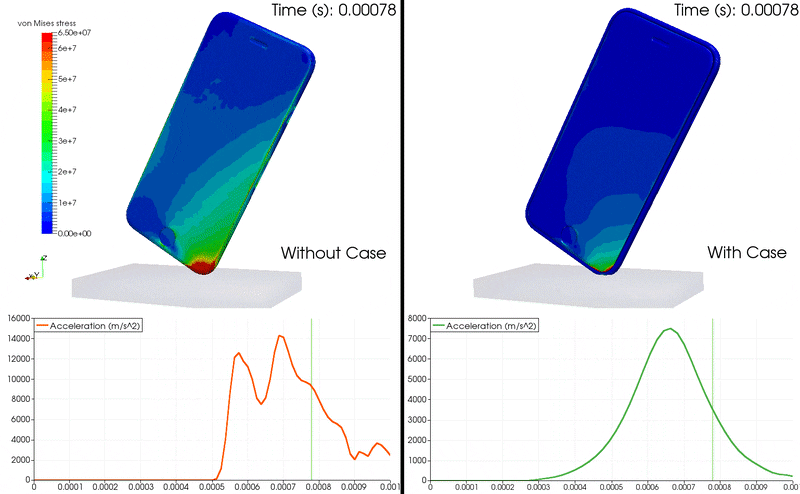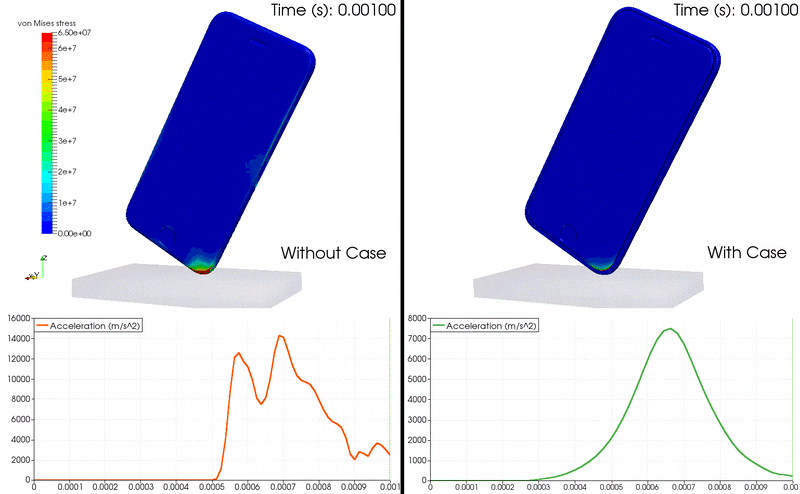
動畫 1:iPhone 掉落 FEA 使用加速度圖顯示 von Mises 應力及其在手機內部的增長。
以上就是本篇的關于有限元的介紹,想了解更多CAE相關信息 歡迎掃碼關注小F(ID:iamfastone)獲取
- END -
我們有個CAE設計研發云平臺
集成多種CAE應用,大量任務多節點并行
應對短時間爆發性需求,連網即用
跑任務快,原來幾個月甚至幾年,現在只需幾小時
5分鐘快速上手,拖拉點選可視化界面,無需代碼
支持高級用戶直接在云端創建集群
掃碼免費試用,送200元體驗金,入股不虧~

更多電子書 歡迎掃碼關注小F(ID:imfastone)獲取

你也許想了解具體的落地場景:
王者帶飛LeDock!開箱即用&一鍵定位分子庫+全流程自動化,3.5小時完成20萬分子對接
這樣跑COMSOL,是不是就可以發Nature了
Auto-Scale這支仙女棒如何大幅提升Virtuoso仿真效率?
1分鐘告訴你用MOE模擬200000個分子要花多少錢
LS-DYNA求解效率深度測評 │ 六種規模,本地VS云端5種不同硬件配置
揭秘20000個VCS任務背后的“搬桌子”系列故事
155個GPU!多云場景下的Amber自由能計算
怎么把需要45天的突發性Fluent仿真計算縮短到4天之內?
5000核大規模OPC上云,效率提升53倍
提速2920倍!用AutoDock Vina對接2800萬個分子
從4天到1.75小時,如何讓Bladed仿真效率提升55倍?
從30天到17小時,如何讓HSPICE仿真效率提升42倍?
關于為應用定義的云平臺:
芯片設計五部曲之二 | 圖靈藝術家——數字IC
芯片設計五部曲之一 | 聲光魔法師——模擬IC
【ICCAD2022】首次公開亮相!國產調度器Fsched,半導體生態1.0,上百家行業用戶最佳實踐
解密一顆芯片設計的全生命周期算力需求
居家辦公=停工?nonono,移動式EDA芯片設計,帶你效率起飛
缺人!缺錢!趕時間!初創IC設計公司如何“絕地求生”?
續集來了:上回那個“吃雞”成功的IC人后來發生了什么?
一次搞懂速石科技三大產品:FCC、FCC-E、FCP
速石科技成三星Foundry國內首家SAFE?云合作伙伴
EDA云平臺49問
億萬打工人的夢:16萬個CPU隨你用
幫助CXO解惑上云成本的迷思,看這篇就夠了
花費4小時5500美元,速石科技躋身全球超算TOP500